2015-11-29
We look at some tricks and considerations that came up during my implementation of Squint.
Squint is a novel online learning algorithm that I recently developed with Tim van Erven (see (Koolen and Van Erven 2015)). In the paper we note that one should be careful when implementing Squint numerically, and give some hints how one might avoid numerical instability. I wanted to do some experiments with Squint myself, and so I recently took the time to implement the algorithm carefully. I made the code available online here. In this post I reflect on my implementation, and talk about some issues that came up and how they were resolved. But let’s start with what Squint is, and what it is for.
Let us first describe the Hedge setting, which is a core online learning task for which Squint is designed.
Prediction proceeds in rounds. In each round \(t\),
the learner plays a probability distribution \(\boldsymbol{w}_t = (w_t^1, w_t^2, \ldots)\) on experts \(k = 1, 2, \ldots\) ,
then the environment reveals the expert losses \(\boldsymbol{\ell}_t = (\ell_t^1, \ell_t^2, \ldots)\),
and the learner incurs the expected loss \(\boldsymbol{w}_t^\intercal\boldsymbol{\ell}_t = \sum_k w_t^k \ell_t^k\).
We denote by \(r_t^k = \boldsymbol{w}_t^\intercal\boldsymbol{\ell}_t - \ell_t^k\) the instantaneous regret of the learner compared to expert \(k\) in round \(t\), and by \(R_T^k = \sum_{t=1}^T r_t^k\) the cumulative regret of the learner compared to expert \(k\) after \(T\) rounds. The goal of the learner is to keep \(R_T^k\) small (or even negative) for all \(k\) and \(T\). If the learner succeeds, this means he behaved almost as well as any expert.
Squint, our strategy for the learner, is parametrised by a prior distribution \(\boldsymbol{\pi}= (\pi^1, \pi^2, \ldots)\) on experts. (I am describing the version from the paper with the improper prior on learning rates.) In addition to the cumulative regret \(R_T^k\) of each expert \(k\), Squint also maintains the cumulative regret squared \(V_T^k = \sum_{t=1}^T (r_t^k)^2\). Then after \(t\) rounds, Squint plays the weights \begin{equation}\label{eq:squint.w} \boldsymbol{w}_{t+1}^k ~=~ \frac{ \pi^k \xi(R_t^k, V_t^k) }{ \sum_k \pi^k \xi(R_t^k, V_t^k) } \end{equation} where \begin{equation}\label{eq:xi} \xi(R,V) ~=~ \int_0^{1/2} e^{\eta R - \eta^2 V} \text{d}\eta . \end{equation} We may think of \(\xi(R, V)\) as the Squint evidence against an expert with cumulative regret \(R\) and regret squared \(V\). With this interpretation, we recognise \(\eqref{eq:squint.w}\) as an instance of Bayes’ Rule with prior \(\boldsymbol{\pi}\) and evidence measured by \(\xi\). The integral in \(\eqref{eq:xi}\) hints at the origin of Squint, which we designed as a method for learning the learning rate \(\eta\).
It can indeed be shown that Squint guarantees small regret. Squint was designed to ensure especially small regret for data with second order and/or quantile luckiness. For bounds, see the paper (Koolen and Van Erven 2015) or my earlier blog post. Squint’s adaptivity, which comes at essentially no computational overhead, makes it a very attractive algorithm for practical applications. In this post we consider the implementation of \(\eqref{eq:xi}\) so that we can play \(\eqref{eq:squint.w}\).
We care to implement the \(\xi\) function from \(\eqref{eq:xi}\) efficiently and numerically stable for all parameter values \(R \in \mathbb R\) and \(V \ge 0\). Our first step is to re-express \(\xi\) in terms of built-in functions \begin{equation}\label{eq:bla} \xi(R,V) ~=~ \sqrt{\pi } \exp \left(\frac{R^2}{4 V}\right) \frac{ \mathop{\mathrm{erfc}}\left(\frac{-R}{2 \sqrt{V}}\right) -\mathop{\mathrm{erfc}}\left(\frac{V-R}{2 \sqrt{V}}\right) }{ 2 \sqrt{V} } \end{equation} Done, right? Well, not quite. Exactly how far we can get with this expression depends on the numerical precision that we have at our disposal. Here is what I found on my laptop.
| \(\mathop{\mathrm{erfc}}\) underflows | \(\mathop{\mathrm{erfc}}\) saturates | \(\exp\) overflows | |
float |
9.19455 | -3.83251 | 88.7228 |
double |
26.5433 | -5.86358 | 709.783 |
long double |
106.536 | -6.47377 | 11356.5 |
Here is a plot for moderate \(R\) and \(V\) (up to a thousand) of how we fare if we evaluate the expression \(\eqref{eq:bla}\) with long double precision. For each subexpression the coloured regions indicate where it can be evaluated accurately. The most constraining operation, precision wise, is the left \(\mathop{\mathrm{erfc}}\) which may saturate when \(R\) gets large compared to \(V\). Can this happen in practice? Unfortunately yes, this happens if there is a good expert with a low prior.
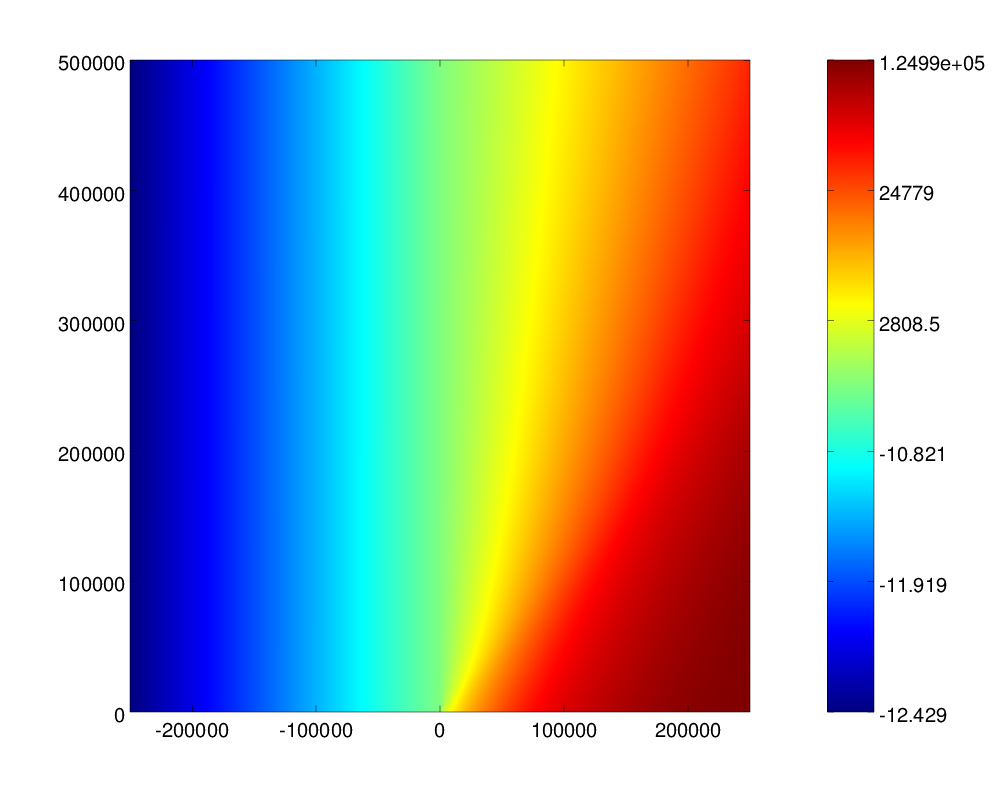
However, the above picture covers too small a region of the parameter space to see all effects. At \(R\) and \(V\) up to half a million (which is still an entirely practical operating regime), the picture looks quite different. The next plot shows that the region where the results of all three operations can be represented with sufficient precision is severely limited. The intersection is a tiny teardrop around the origin.
Thinking about precision, one more problem rears its head, namely that \(\xi(R, V)\) may get extremely large. In fact, in the lower-right corner of the above plot the value \(\xi(R, V)\) overflows the range of numbers representable by long double. Trouble.
As the function \(\xi\) is non-negative, a solution to this problems is to instead compute \[\ln \xi(R, V) .\] So how do we do that? Again starting from the above expression \(\eqref{eq:bla}\) for \(\xi\), it would be really useful to have an implementation of \(\ln(\mathop{\mathrm{erfc}}(x))\). That is not typically built-in (it is not part of C99, or of MATLAB). So in the next section we discuss implementation of \(\ln (\mathop{\mathrm{erfc}}(x))\), and then we continue with Squint.
The function \(\mathop{\mathrm{erfc}}(x)\) tends to \(0\) from above for large \(x\). Here we take a look at computing its logarithm \(\ln(\mathop{\mathrm{erfc}}(x))\). As we are interested in large \(x\), we may use a continued fraction expansion around \(x = \infty\) to obtain \begin{align*} \ln(\mathop{\mathrm{erfc}}(x)) &~=~ -x^2 - \log(\sqrt{\pi} x) + \frac{1}{f_1(x)} \\ f_1(x) &~=~ -\frac{5}{2} -2 x^2 + \frac{1}{ f_2(x) } \\ f_2(x) &~=~ \frac{6078}{5329} + \frac{24}{73} x^2 + \frac{1}{ f_3(x) } \\ f_3(x) &~=~ -\frac{68398632573865}{20616238623752} -\frac{1945085}{3210626} x^2 +\frac{1}{ f_4(x) } \\ f_4(x) &~=~ \frac{159978434211051272742519351345635992}{136120281666497321297368508881328169} +\frac{926674444466713442528}{5898320869008200456169} x^2 + \frac{1}{f_5(x)} \\ &~~\vdots~~ \end{align*} By truncating this expansion we get an approximation. We obtain the \(i\)th order approximation to \(\ln(\mathop{\mathrm{erfc}}(x))\) by replacing \(f_{i+1}\) by \(\infty\). The plot below shows how good such approximations are.
The conclusion is that with order \(4\) we reach \(14\) decimal digits of accuracy well before \(x=10\). For \(x \le 10\) we can instead use the expression \(\ln(\mathop{\mathrm{erfc}}(x))\) directly.
Let us continue with implementing Squint. Using \(\eqref{eq:bla}\), our starting point is \[\ln \xi(R, V) ~=~ \frac{\ln \pi}{2} + \frac{R^2}{4 V} + \ln \left( \mathop{\mathrm{erfc}}\left(\frac{-R}{2 \sqrt{V}}\right) -\mathop{\mathrm{erfc}}\left(\frac{V-R}{2 \sqrt{V}}\right) \right) - \ln (2 \sqrt{V}) .\] We would still lose all precision if we compute the difference of \(\mathop{\mathrm{erfc}}\)s directly. To circumvent this we use the “log-sum” trick; for any \(x > y\), \[\ln(x-y) ~=~ \ln (e^{\ln x} - e^{\ln y}) ~=~ x + \ln (1 - e^{\ln y - \ln x}) .\] By combining the “log-sum” trick with the implementation of \(\ln \mathop{\mathrm{erfc}}(x)\) outlined above, we can compute the Squint log-evidence term \(\ln \xi(R, V)\) already quite generally. Two more details need to be sorted out to get to an implementation that works for all parameter values \(R\) and \(V\).
The \(\ln\mathop{\mathrm{erfc}}(x)\) implementation was designed to be precise for \(x>0\). But what if either or both \(\mathop{\mathrm{erfc}}\) arguments are negative? Then we can use the reflection formula \[\mathop{\mathrm{erfc}}(-x) ~=~ 1-\mathop{\mathrm{erf}}(-x) ~=~ 1+\mathop{\mathrm{erf}}(x) ~=~ %2+\erf(x)-1 %~=~ 2 - \mathop{\mathrm{erfc}}(x)\] to flip the sign of \(x\). If both arguments were negative, we need to flip both and the \(2\)’s cancel. If only one argument was negative we can evaluate the argument of the \(\ln\) directly.
Finally, we need to worry about small \(V\). Our original formula \(\eqref{eq:xi}\) is fine for small \(V \approx 0\) (we may even plug in \(V=0\) without issue). This is no longer true of \(\eqref{eq:bla}\). So we introduce a special case for small \(V\), and approximate \[\ln \xi(R, V) ~\approx~ \ln \frac{e^{R/2-V/4}-1}{R-V/2} \qquad \text{for small $V$} .\] This introduces another worrisome case, namely \(R \approx V/2\). There we use \[\ln \xi(R, V) ~\approx~ R/2-V/4 - \ln(2) \qquad \text{for small $V$ and $R \approx V/2$} .\]
Using the above tricks, we arrive at an implementation of \(\ln \xi(R, V)\) and hence of the Squint log-evidence that is accurate to more than 15 decimal places (as far as one can tell by comparing to other, more direct expressions that are accurate only for limited ranges). The code is available here.
Let me conclude by showing a plot of \(\ln \xi(R,V)\) for a large range of \(R\) and \(V\). I had to make the colormap non-linear, otherwise all action would only be in the lower-right corner.